 Imprimir|Regresar a la nota
Imprimir|Regresar a la notaQuiero empezar planteando un problema ingenuo, pero le sugiero que no crea que porque escribo “ingenuo” se transforma automáticamente en trivial. No. La solución no es inmediata pero lo que puedo asegurar es que cualquier persona puede abordarlo, pensarlo y encontrar la respuesta. No hace falta saber nada particular. No hace falta ser especialista en nada y, en todo caso, muestra cómo muchas veces nos embarcamos en establecer fronteras artificiales que en la vida real no existen. Me explico: uno aprende en el colegio/escuela a resolver problemas de matemática, de física, de química, de biología, de geología, etc., etc., pero los problemas en la vida cotidiana no vienen con una “etiqueta” que los separa o distingue. Entonces, cuando llega el momento de enfrentar una situación cualquiera en donde se requiere pensar, no sirve –en general– tratar de recordar lo que uno estudió, sino tratar de “crear” y buscar alternativas de solución desde cualquier ángulo posible.
Por eso es que todas las empresas (y los gobiernos) debieran abordar los problemas con gente que llegue entrenada en distintas disciplinas: poner lo que hay que resolver sobre la mesa y discutir entre todos. La idea consiste en superar los obstáculos independientemente de las herramientas que hagan falta. Si me permite una reflexión al respecto, diría que valoro mucho más la capacidad creativa que la cultura enciclopedista, que suele apuntar a “amontonar” información, aprender e incorporar datos en forma indiscriminada.
La vida viene preparada de otra manera: uno primero tiene problemas, y después busca las soluciones, y no al revés, como suele suceder en la mayoría de las currículas escolares, en donde uno aprende soluciones a problemas que no tiene, estudia teorías para contestar preguntas que no se hizo, y por supuesto, se las olvida ni bien pudo salir de la presión social que representa “tener que aprobar”.
Pero me desvié. Quiero volver al problema. Es un problema precioso que fue presentado hace un par de años por el matemático español Adolfo Quirós. Es obvio entonces que todo el crédito le corresponde a él, así como la belleza de la solución que voy a proponer más abajo. Me apuro en decir (otra vez) que, como usted descubrirá después, no hace falta ningún conocimiento específico. Lo único que es necesario es pensar.
Suponga que tiene el siguiente mapa con 11 ciudades diferentes. Algunas de las ciudades están unidas por carreteras. Otras no. Las numeré de manera tal de hacer el texto más sencillo. La carretera entre un par de ciudades está indicada por un segmento que las une.
El objetivo es empezar en una ciudad cualquiera (usted elige) y tratar de pasar por todas “una sola vez” y volver a la ciudad de partida.
No es necesario utilizar “todos” los caminos. Pueden quedar algunas carreteras sin utilizar, pero lo que sí, es que cada ciudad debe ser visitada exactamente una vez antes de volver al punto de partida. Este es el dibujo:
Figura 1
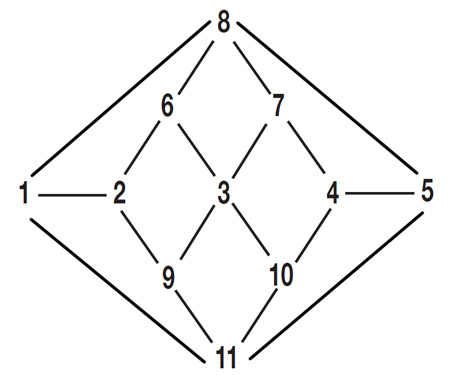
¿Se puede? ¿Existe algún camino que usted pueda trazar y que cumpla con las condiciones expuestas más arriba? Si es así, escriba el “orden” en el que hay que recorrer las ciudades.
Si usted concluye que no es posible encontrar el camino, no alcanza con que usted diga “no existe porque yo no lo encontré”. Eso dejaría la posibilidad abierta de que viniera otra persona y sí pueda hallar lo que usted no pudo. Sin embargo, en matemática, cuando uno dice que “tal problema no tiene solución”, lo que uno está diciendo es que no importa el tiempo que pase, ni quién venga, esa solución no va a poder ser encontrada, y para eso, es necesario “demostrar” que la tal solución no existe.
Ahora, como siempre, le toca a usted.
Para convencerse de que no existe (ni existirá) una solución al problema, le propongo que hagamos lo siguiente. Voy a poner un círculo alrededor de algunos números (ciudades) y a otros los voy a enmarcar en un cuadrado. ¿Cómo decidir a cuáles ponerles un círculo y a cuáles un cuadrado? Si dos números están conectados por un camino, entonces uno debe tener un círculo y el otro un cuadrado, o sea, tienen que tener dos figuras geométricas distintas alrededor. Por ejemplo, como le puse un círculo al 1, entonces el 2 (que está conectado con el 1) tiene que tener un cuadrado. Pero como el 2 tiene un cuadrado y está conectado tanto con el 6 como con el 9, entonces ambos tienen que tener un círculo. De la misma forma, el 3 y el 8 tienen que tener un círculo, porque están conectados con el 6 que tiene un cuadrado. Y así siguiendo. Más aún: le sugiero que tome la Figura 1 que está más arriba, en donde aparece el planteo del problema, y haga usted la distribución de los círculos y los cuadrados. Verá que obtiene el mismo resultado: tendrán círculos los números 1, 6, 7, 9, 10 y 5, mientras que quedarán con cuadrados el 2, 3, 4, 8 y 11. O al revés: quedarán con cuadrados alrededor el 1, 6, 7, 9, 10 y 5 mientras que tendrán un círculo el 2, 3, 4, 8 y 11. De acuerdo con lo que yo hice en la Figura 2, hay seis números que tienen círculos y cinco que tienen un cuadrado.
Dicho esto, quiero que pensemos juntos algo más que será muy importante: cada vez que caminamos de una ciudad a otra (o bien, de un número a otro), pasamos de un número que tiene un círculo a otro que tiene un cuadrado. O al revés. Es decir, vamos alternando números que tienen un círculo con números que tienen un cuadrado.
Ahora llegó el momento interesante en donde vamos a concluir que el camino que queremos construir no puede existir. ¿Por qué? Como el total de ciudades es 11, entonces usted tendrá que dar 11 pasos para recorrerlas todas y volver a la de partida. Es importante que me siga con este último argumento. Como usted empieza “parado” en algún número, tendrá que dar en total 11 pasos hasta volver al punto inicial (que le permitirá recorrer una vez por cada ciudad que no es la de partida, pero tendrá que volver al lugar inicial). Por eso son 11 pasos. Voy a llamar (CIR) a los números que tienen un círculo y (CUA) a los que tienen un cuadrado. Digamos que empieza parado en un número que tiene un círculo (CIR), cuando da el primer paso llega a un número (CUA). Cuando da el segundo paso llega a un número con un círculo (CIR), y al seguir caminando va alternando (CIR) con (CUA). Como escribí recién, uno tiene que dar en total once pasos.
Fíjese que cada vez que dio un número par de pasos llega a un (CIR). Cuando dio un número impar de pasos, llega a un número (CUA). Y eso debería ser suficiente para convencerla/o de que el camino no va a existir. ¿Quiere pensarlo usted en soledad?
Es que como tenemos que dar once pasos, que es un número impar de pasos y empezamos en un número (CIR), llegaríamos a uno que es (CUA), y eso demuestra que el camino que queremos construir no va a existir, porque el objetivo es llegar a la misma ciudad de partida pasando una sola vez por cada ciudad/número. Por lo tanto, no importa qué camino pretendamos construir, será imposible encontrarlo.
Como se ve, la solución es verdaderamente sencilla. Todo lo que uno tiene que hacer es descubrir que el número de pasos que tiene que dar es impar, y, que si sale de un número con un “círculo”, en un número impar de pasos (que son los 11 que tenemos que dar) llegará a uno con un “cuadrado” alrededor y por lo tanto, no podrá nunca llegar a la ciudad en la que empezó. Y eso concluye la demostración.
Figura 2

Este tipo de problemas forman parte de una preciosa rama de la matemática que se conoce con el nombre de Teoría de Grafos. No es este el lugar para que yo escriba sobre el tema (ni tampoco tengo la experiencia ni el conocimiento para hacerlo), pero la literatura es vasta y los resultados son espectaculares. Además, tiene una utilidad tremenda en biología, física, ingeniería, en ciencias sociales, en informática (muy especialmente), etc., etc.
La existencia o no de cierto de caminos suelen ser problemas altamente no triviales. De hecho, el 18 de mayo del 2006, apareció en la contratapa de Página/12 un problema “abierto” (o sea, sin solución aún) y que es el más famoso del mundo al respecto: el que se conoce con el nombre de El Viajante de Comercio. Cualquier persona que logre resolver el problema del Viajante de Comercio pasará a ser millonario instantáneamente, porque hay por lo menos una recompensa de un millón de dólares para quien lo resuelva, pero más importante aún (creo), se transformará en una de las personas más famosas de este siglo (en términos de reconocimiento científico, sin ninguna duda).
Para terminar, el primer artículo de esta serie que publiqué en Página/12 (el 6 de noviembre de 2005) fue justamente el que se considera el problema que dio origen a la Teoría de Grafos. Fue resuelto por uno de los matemáticos más importantes de la historia,
Leonhard Euler (1707-1783). Si le interesa, entonces, pensar problemas de este tipo, allí puede encontrar otro que también es muy famoso.
En la edición del último domingo 13 de abril apareció un error en los gráficos que acompañaban a la nota de la contratapa.
Con el planteo que figuraba en el diario, no es necesario argumentar como hice yo para concluir que no es posible encontrar el camino que se pedía, sino que había formas muchísimo más sencillas.
El objetivo era trazar un camino que pasara por todas las ciudades una sola vez y regresar al punto de partida. Tomemos por ejemplo la ciudad que figura con el número 1. Si hubiera una sola ruta (que la comunica con 2 como figuraba en el dibujo del domingo), esa ciudad no podría estar en ningún camino intermedio porque para llegar hasta ella (la número 1) hay que pasar inexorablemente por 2, pero al salir, hay que repetir el camino de entrada, y por lo tanto, visitar la número 2 otra vez. Conclusión: la número 1 no puede ser una ciudad intermedia.
Pero casi con el mismo argumento se puede concluir que la ciudad 1 no puede ser la ciudad inicial. Si lo fuera, debería ser la final también, por lo que el camino que la une con 2 hay que recorrerlo tanto a la ida como a la vuelta, pasando dos veces por la ciudad 2.
Es decir, el error en el dibujo transformó en superfluo e innecesario tanto esfuerzo para explicar la imposibilidad de encontrar el tal camino. Mis disculpas. En todo caso, si aún tiene ganas de concederme/se una nueva oportunidad, fíjese en el dibujo correcto que acompaña esta errata y trate de demostrar que aún así es imposible encontrar una ruta que pase por todas las ciudades una sola vez y vuelva al punto de partida.
El ejercicio sigue teniendo la misma validez del domingo; mi cerebro quizás, ya no.
© 2000-2022 www.pagina12.com.ar|República Argentina|Todos los Derechos Reservados
Sitio desarrollado con software libre GNU/Linux.