[cerrar]

Comparta esta nota con un amigo

E-Mail de su amigo
Su nombre
Su E-Mail

Uno de los placeres que la mayoría de la gente se roba a si misma, es la oportunidad de poder entretenerse pensando mientras resuelve problemas parecidos al Sudoku. ¡Espere! No se vaya todavía. Deme una chance. Permítame -o mejor dicho, permítase- avanzar un poco más en esta lectura y en todo caso, siempre puede abandonar... pero deme la oportunidad de mostrarle algo que usted también puede hacer y que no solo le servirá para incrementar su auto-estima, sino también para entretenerse genuinamente.

En todo caso, todo lo que tiene que hacer es leer el problema e inmediatamente después, la solución, pero lo que quiero hacer, es mostrarle cómo lo fui pensando yo.... paso por paso. Para el final me reservo una pregunta, y es por eso que le pido que no me abandone... aún. Acá voy.

Supongamos que yo le doy una grilla de 3 x 3, como si fuera un tablero de ajedrez, pero de 3 x 3. Al mismo tiempo, le entrego 9 bolitas de cuatro colores diferentes: rojo, azul, verde y amarillo.

Se trata de distribuirlas en el tablero de manera tal que se cumplan las siguientes reglas:

1) Tiene que haber una roja en la primera o segunda fila.

2) Tiene que haber 2 verdes en la tercera columna.

3) Las amarillas solamente pueden ocupar las esquinas, y en total hay tres de este color.

4) Dos de las azules tienen que estar en la segunda fila.

5) Tiene que haber al menos una verde por fila.

Preguntas:

a) ¿Cómo se puede hacer la distribución de las bolitas?

b) ¿Cuántas soluciones posibles hay?

Como ve, el problema es sencillo. Piénselo por su cuenta. En cualquier caso, le propongo que me siga, paso por paso y verá que no solo usted estaría/está en condiciones de resolverlo, sino que apostaría a que usted tiene sus propias ideas que le servirían para llegar al resultado en forma mucho más rápida. Primero le toca a usted.

Mis ideas

Lo primero que quiero saber es cuántas bolitas hay de cada color. Veamos.

De la primera frase, es seguro que tiene que haber por lo menos una roja.

De la segunda frase, es seguro que tiene que haber por lo menos dos verdes

De la tercera frase, es seguro que tiene que haber exactamente tres amarillas.

Antes de avanzar, ya sabemos el color de seis bolitas: una roja, dos verdes y tres amarillas...

De la cuarta frase, se deduce que por lo menos tiene que haber dos azules. Con este dato, ya sabemos el color de ocho de las bolitas. ¿Y la novena?

Fíjese que la quinta frase dice que tiene que haber una verde por fila. Por lo tanto, esto implica que las verdes ¡tienen que ser por lo menos tres!

Y listo. Ya no hay más lugar; ya sabemos el color de las nueve:

3 verdes, 3 amarillas, 2 azules y 1 roja.

El problema es encontrar la distribución. Empecemos.

Como las amarillas solamente pueden ocupar las esquinas y hay exactamente tres, el tablero puede adoptar nada más que cuatro posiciones:

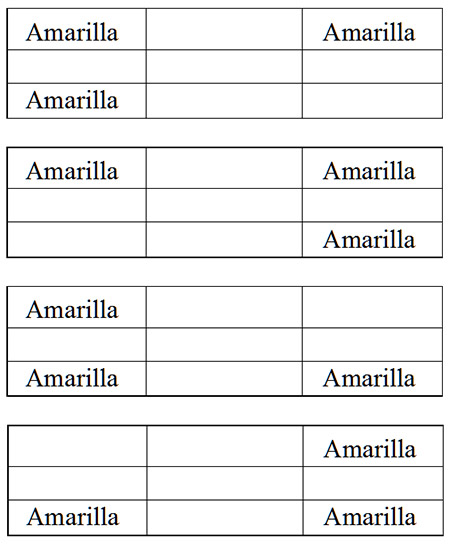
Sin embargo, como la segunda frase dice que tiene que haber dos verdes en la tercera columna, eso descarta que pueda haber dos amarillas allí y en consecuencia podemos tachar dos de las cuatro. Quedan estas dos:

O si no...

Como sabemos que tiene que haber dos azules en la segunda fila (por la cuarta frase), las ubico en cada uno de los casos posibles. Quedan así:

O si no...

Por la primera frase, ya sabemos de qué color es la bolita que falta en la primera fila: roja. Luego, las dos posibilidades siguen siendo estas dos:

O si no...

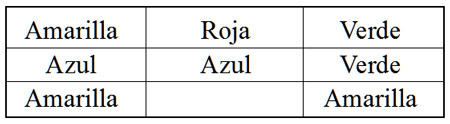
¿Y ahora? ¿Cómo distinguir cuál de las dos posibilidades termina el problema? ¿O sirven las dos?¿Y por qué?

Por la distribución de colores, ya sabemos que la bolita que falta tiene que ser de color verde, y justamente, la última frase dice que ¡tiene que haber al menos una verde por fila! Si usted se fija en las dos posiciones posibles, verá que la primera de ellas no contiene ninguna bolilla verde y no hay lugar para que la incorpore. En cambio, el segundo tablero sí lo permite. La agrego allí y descarto el otro. Queda así:

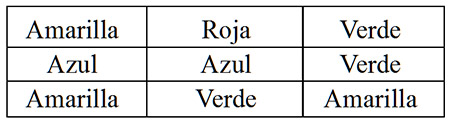
Un par de reflexiones finales

a) Habrá descubierto que no hay más que esta solución. La construí descartando cualquier otra posibilidad. Es por eso que podemos afirmar, usted y yo, que la solución ¡es única!

b) Espero que haya llegado hasta acá, ya sea “usándome” a mí, o en soledad, pero en cualquier caso tengo una pregunta: ¿no lo podría haber hecho usted por su cuenta? ¿hay algo de lo que leyó acá arriba que la (o lo) invitó a pensar: esto que hace este hombre, a mí....¡no se me hubiera ocurrido nunca! ¿Es así? ¿Le pasó eso en alguna instancia de este desarrollo?

No, creo que usted detecta que todo lo que está escrito no solo está a su alcance sino que al final termina siendo muy sencillo. Y ese era mi objetivo.

Mucha gente se “roba” a sí misma la posibilidad de entretenerse, pero además, se ubican a si mismos en una categoría como si fueran “inferiores” en tanto que seres pensantes. ¡Esto no es para mí! ¡Una locura!

TODO el mundo está en condiciones de entender esto y no hay derecho ni a hacérselo a uno mismo, ni tolerar que se lo hagan a otros. ¿Usted qué piensa?