![]()
![]()
![]() Miércoles, 24 de septiembre de 2008
| Hoy
Miércoles, 24 de septiembre de 2008
| Hoy
CIENCIA › UN PROYECTO QUE REPRODUCE LO QUE HIZO ERATóSTENES HACE MáS DE DOS MIL AñOS
Medir la circunferencia de la Tierra
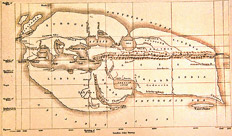
El Proyecto Eratóstenes, que lleva adelante la Facultad de Ciencias Exactas y Naturales (UBA), reproduce la hazaña del gran científico griego (Cirene 276 a.C.-Alejandría 194 a.C.), que midió por primera vez la circunferencia terrestre.
 Por Leonardo Moledo
Por Leonardo Moledo
El jinete está desconcertado. Acostumbrado al diálogo, se encuentra ahora con un ménage-à-quatre. En efecto, aquí están con él tres físicos: Silvina Ponce Dawson, directora del Departamento de Física de la Facultad de Ciencias Exactas y Naturales (UBA, naturalmente); Victoria Bekeris, que coordina el proyecto con la Asociación Física Argentina, y Guillermo Mattei, que se ocupa de las actividades de difusión del departamento y coordina la logística de la organización del proyecto, a quienes debe confesarles un olvido, como se verá.
–Son muchos, así que el que quiera puede empezar a contarme en qué consiste el Proyecto Eratóstenes. Además, me olvidé de pedir un fotógrafo, así que no voy a tener más remedio que poner una ilustración alusiva a Eratóstenes. Ustedes no van a aparecer, pero piensen que en su lugar va a estar nada menos que Eratóstenes.
Victoria Bekeris: –El proyecto consiste en tratar de medir el radio de la Tierra como lo hizo Eratóstenes hace más de veinte siglos, haciendo que participen escuelas de todo el país. Lo interesante es que sí o sí tienen que participar escuelas de dos puntos diferentes, ubicadas sobre el mismo meridiano. Es una medición bastante fácil...
–Es la que hizo Eratóstenes...
V. B.: –Es una adaptación de la que hizo él. Porque en realidad él midió el 21 de junio, que es cuando empieza el verano en el Hemisferio Norte. El vivía en Alejandría y notaba que en Siena había un pozo donde el sol entraba tan verticalmente que entraba exacto dentro del pozo. Simultáneamente, en Alejandría, los rayos en el mismo momento tenían una inclinación diferente (puesto que proyectaban sombra). A partir de eso, hizo una deducción según la cual calculó que la Tierra estaba curvada y definió su radio.
–Hay un problema allí, que es que Eratóstenes definió la circunferencia en estadios. Si el estadio es el estadio egipcio, la diferencia con la cifra que manejamos ahora es mínima. Si es el estadio griego (el de 185 m) es bastante distinto (un 17 por ciento, para ser más precisos).
V. B.: –En ese caso, él tenía una de las ciudades justo en el trópico. Como nosotros no tenemos ninguna, adaptamos el experimento y pensamos en dos Alejandrías, que están ubicadas en distintas latitudes. A través de las sombras que proyectan al mediodía, se pueden calcular los ángulos de incidencia de los rayos. Son dos ciudades, dos grupos de chicos de escuela, que miden la sombra de un palito en el mediodía solar y comparten esas mediciones.
–Y tienen que calcular el ángulo entre la sombra y el palito. ¿Cómo se hace eso?
V. B.: –Una de las formas era dibujar el triángulo que se les presentaba en un papel milimetrado y después con un transportador medir el ángulo. La otra era mediante la trigonometría. Eso depende de cuánto sepan los chicos.
Silvina Ponce Dawson: –Como está planteado para escuelas medias, se supone que se puede usar trigonometría.
–De todos modos, creo que lo importante allí no es el uso o no de trigonometría, sino la sensación de estar haciendo lo mismo que Eratóstenes, que es una de las cosas más geniales que se pueden imaginar. Sin aparatos, con una varilla y con camellos (con los cuales midió la distancia entre Siena y Alejandría).
S. P. D.: –No sólo eso, sino la colaboración, la sensación de ser parte de un proyecto colectivo...
Guillermo Mattei: –Como dicen ustedes, las reacciones de las escuelas fueron muy buenas. Estaban desesperados porque estaba nublado y no salía el sol. Había un furor increíble. A partir de una abstracción matemática tan sencilla poder llegar a calcular el tamaño del planeta sobre el que uno vive es algo espectacular. Hay 114 escuelas que quisieron participar (aunque después hay que ver cuántas terminan efectivamente pasando los datos). Hay unos 3200 chicos involucrados. Ese espíritu de repetir lo hecho por Eratóstenes creo que se logró transmitir...
S. P. D.: –Y a lo largo de un territorio vastísimo. Hay escuelas participantes desde Tierra del Fuego hasta Tucumán.
–Además, es un experimento sobrecogedor. Ya se sabía que la Tierra era esférica, pero medirla fue un paso impresionante. E hizo que científicos celosos corrigieran esa cifra al voleo. Tolomeo, por ejemplo. La fueron bajando. Tolomeo bajó la cifra, y esa cifra fue la que usó Colón, bajándola todavía más, hasta el punto que Japón quedaba a la altura de Cuba. Esa fue la verdadera discusión, no si la Tierra era redonda o plana. Todo el mundo sabía que era esférica, incluso había un globo terráqueo. Toda esa inmersión en la historia es interesante.
V. B.: –Y les permite entender de dónde vienen y cómo son los rayos del sol, por ejemplo. No es sólo la historia. Entender por qué es de día o de noche, la utilidad de la matemática para entender esos fenómenos naturales. Y la posibilidad de abstraer, de presentar a escala humana algo que está en una escala muchísimo mayor.
–Y, además, con una cosa muy local abarcan la circunferencia de todo el planeta. Eso es verdaderamente muy impresionante.
S. P. D.: –Nosotros hicimos un experimento entre nosotros, antes de lanzar este proyecto, en que medimos estas cosas. Cuando uno va midiendo, para ver cuál es el mediodía solar, la sombra va cambiando de longitud y uno puede percibir claramente la rotación de la Tierra. Los chicos deben haber sentido eso. Es una conexión increíble con el universo físico.
V. B.: –Y con la naturaleza astronómica. Es disparador de muchas cosas.
–¿Después de esto qué viene?
S. P. D.: –La idea es, el año que viene (que es el Año Internacional de la Astronomía), hacerlo con más escuelas. Esto lo hicimos bastante a las apuradas, no pensamos jamás que iba a tener tal repercusión y tal cantidad de gente participando. Lo habíamos tomado como una prueba piloto para lo que venía el año que viene. Y también queríamos probar otras experiencias.
–Se podría, por ejemplo, medir la distancia a la luna con un láser. Pasa que para eso es necesario un reloj de precisión.
S. P. D.: –A nosotros lo que nos entusiasmó mucho fue la idea de los chicos colaborando en diferentes partes del país.
–¿Y medir la velocidad de la luz? Hay un montón de experimentos históricos que se pueden hacer. Alguien en el siglo XII no tenía las cosas que tenemos ahora. A ver, Guillermo... ¿Por qué no me cuenta un poco su experiencia de difusión?
G. M.: –Bueno, el departamento participa en muchísimas actividades: la semana de la ciencia, charlas en las escuelas, mostrando experimentos en el Planetario. El tema de vincularse con la escuela media me parece que es una asignatura pendiente.
V. B.: –Ahora, por ejemplo, estamos armando unos cd. Porque en la página web fuimos cargando temas de física en relación con la actualidad: en el año 2005, que fue el año de Einstein, trabajamos con la relatividad; en el 2006, con el mundial de fútbol, cargamos contenidos vinculados con cómo se mueve la pelota (incluso el chico que armó esa página estuvo en Fox Sports el día que no hubo partidos). Nuestra idea es instalarnos como un lugar de contenidos en física, para el uso tanto en escuela media como un público en general.
–Hay otra experiencia... medir el tiempo de caída de algún objeto de una altura de, pongamos, 2 o 3 metros, y de ahí deducir cuánto tarda la luna en dar la vuelta. Que más o menos tiene que dar. Ese es el cálculo que hizo Newton... Y tiene que dar una cosa bastante parecida a 28 días. Lo más importante de todo esto, creo yo, es que los chicos se den cuenta de que todas estas cosas ocurren también fuera del laboratorio. Da la sensación de que, en la escuela media, la ciencia queda reducida al espacio del laboratorio y que la física funciona solamente adentro del colegio. Cuando los chicos salen, el mundo vuelve a ser aristotélico.
G. M.: –Acá nosotros tenemos la campana de vacío. Y usted se acordará, cuando la llevábamos al Planetario, la impresión que causaba que una pluma cayera a la misma velocidad que una piedra.
–Sí, era alucinante.
G. M.: –Porque una cosa es que aparezca en los libros y otra muy distinta enfrentarlo cara a cara.
–Lo lindo, como ustedes dicen, es probar todos estos experimentos en una red de colaboración.
G. M.: –Por la distribución geográfica de las escuelas, es difícil que estén en el mismo meridiano. Para eso, entusiasmamos a un grupo de investigación de matemáticos para minimizar la distancia en longitud y en los días de medida.
–¿No miden el mismo día?
V. B.: –La idea es que sí, pero como puede estar nublado en algunos lugares y en otros no, dimos una semana. Calculamos que el error iba a ser pequeño.
–Claro, porque si no es muy descorazonador. ¿Y qué resultados tuvieron las escuelas que lo hicieron?
G. M.: –Bastante aproximados. Algunas cosas detectamos que se podrían haber medido mal, que podrían haberse filtrado algunos errores.
S. P. D.: –Yo de lo que tenía miedo era de que se trucharan los datos para llegar a valores similares a los que queríamos buscar. Pero lo que nos interesaba no era eso, sino el proceso de medición. En ese sentido, la equivocación nos revela que fueron honestos y que le dieron más importancia al proceso de medición que a los resultados que se esperaba obtener.
V. B.: –Por otro lado, una de las cosas que les cuesta a los profesores es admitir que se equivocan: son los que “traen la verdad” a las aulas, y muchas veces es difícil para ellos reconocer los propios errores. Una experiencia como ésta va a abrir un poco la mentalidad de todos.
G. M.: –Y, además, se promueve la interrelación y la discusión entre docentes.
-
UN PROYECTO QUE REPRODUCE LO QUE HIZO ERATóSTENES HACE MáS DE DOS MIL AñOS
Medir la circunferencia de la Tierra
Por Leonardo Moledo
ESCRIBEN HOY
- Adrián De Benedictis
- Adrián Soto
- Alejandro López Accotto, Rubén Seijo y Carlos Martínez
- Alfredo Zaiat
- C. C.
- Carlos Rodríguez
- Cledis Candelaresi
- Cristian Carrillo
- Cristian Vitale
- Daniel Miguez
- Emanuel Respighi
- Facundo García
- Fernando Krakowiak
- Guillermo Zysman
- Horacio Bernades
- Horacio Cecchi
- Jorge Isaías
- Julián Bruschtein
- Leandro Arteaga
- Leonard Doyle
- Leonardo Moledo
- Luciano Sanguinetti
- Martín Piqué
- Miguel Jorquera
- Nora Veiras
- Raúl Dellatorre
- Roberto Follari
- Rocco Carbone
- Rodrigo Fresán
- Roque Casciero
- Sebastian Abrevaya
- Sebastián Ochoa
- Sebastián Premici y Miguel Jorquera
- Silvina Friera
- Tomás Lukin
- Walter Oppenheimer
- Werner Pertot
© 2000-2022 www.pagina12.com.ar | República Argentina | Política de privacidad | Todos los Derechos Reservados
Sitio desarrollado con software libre GNU/Linux.






