[cerrar]

Comparta esta nota con un amigo

E-Mail de su amigo
Su nombre
Su E-Mail

Las historias que requieren de un detective suelen ser siempre muy intrigantes y atractivas. Esto sucede tanto en nuestras vidas cotidianas, como en las películas o series que llevan un nombre: “policiales”. Es decir, muchísima gente ha mirado o mira series de televisión en donde la idea es tratar de descubrir al asesino o su equivalente. Se trata en todo caso de juntar los “datos” que son esparcidos por los guionistas a lo largo de la película para ver si uno tiene la capacidad de relacionarlos, combinarlos e inferir quién fue.

Por supuesto, hay buenas y malas películas, de eso no tengo dudas. Pero no me refiero solo a las actuaciones de actores y actrices, sino a las tramas subyacentes. No voy a ser yo quien le advierta de la multiplicidad de trampas que pululan, de manera tal que cuando uno cree que tiene todo lo que le hace falta para poder deducir “quién fue”, súbitamente aparece algo escondido, algo no sabido, o algo totalmente retorcido. Pero aun cuando eso no suceda, aun contando con la buena fe de quien escribió los textos, muchas veces pasa que uno descubre que “a mí esto no se me hubiera ocurrido nunca” porque hay algo “que no pega”. En fin, me estoy extendiendo demasiado en algo que se me ocurre que a esta altura usted comprendió de qué estoy hablando.

Pero lo que sí quiero es relacionar esto que escribí más arriba con un policial de la matemática. Muchas veces se trata de inferir qué sucede o qué sucedió sin que los datos sean directos. La idea es tratar de relacionarlos, combinarlos, imaginar diferentes escenarios, elaborar alguna estrategia y fijarse si el producido final es lo que uno estaba buscando. Claro, una cosa es un “policial” en un cine o en televisión y otra –aparentemente bien distinta– es un problema de matemática, o de matemática recreativa.

Lo que quiero hacer es proponerle entonces un dilema para dilucidar. Yo hago el planteo y usted busca descubrir quiénes son los “asesinos”. En el camino, voy a tratar de mostrarle cómo se puede introducir lo que se llama “un grafo” (o una suerte de dibujo) para hacerle la vida más fácil; pero me estoy apurando. Avancemos con el problema y después hablamos de la solución o de la forma de pensarlo. Acá va.

Suponga que la policía detiene a seis personas. Sabe que dos de ellos fueron los autores de un robo. Las voy a llamar A, B, C, D, E y F. La presión va en aumento y comienza el interrogatorio en forma separada. Es decir, cada uno de ellos contesta en una habitación diferente sin que los otros sepan qué está confesando (o no).

Uno de los seis se niega a declarar. No le importa la pena que le den: no quiere delatar a nadie. Los otros cinco sí contestan. Cada uno de los cinco restantes entrega dos nombres (o dos letras) que se supone que incriminan a sus otros compañeros. De todas formas, los policías saben que:

a) Uno sólo de ellos (de los cinco que contestan) da dos nombres falsos. Es decir, nombra dos compañeros que no fueron los autores.

b) Los otros cuatro también dan dos nombres, pero con la particularidad de que cada uno de ellos da un dato verdadero y otro falso.

Estas fueron las respuestas, sin indicar quién las fue dando ni tampoco quién fue el que dio dos nombres falsos:

1) AB
2) AD
3) AE
4) CD
5) CF

Solo para ratificar que usted me entiende el planteo, fíjese que cuando digo que uno de ellos contestó AE, esto significa que él está acusando a A y a E. Lo mismo con los otros.

Dicho esto, ¿se anima a deducir quiénes fueron los autores del robo? Lo que yo puedo hacer desde acá es decirle que sí, que se puede descubrir, pero hace falta hilvanar algunos razonamientos. Esta parte entonces se la dejo a usted. Yo sigo más abajo con algunas reflexiones.

Idea para pensar cómo resolver el dilema

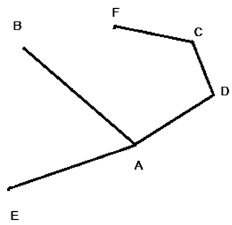
¿Qué es este dibujo? Lo único que hice fue escribir los “nombres” (las letras) de cada uno de los presentes. Los segmentos que los unen son los que corresponden a las respuestas que fueron dando cada uno. Es decir, como uno de ellos contestó AB, entonces tiene que haber un segmento que los una (y lo “hay”). De la misma forma, cada respuesta se corresponde con una línea que une a esas dos personas.

Dicho esto, ahora avancemos para ver si somos capaces de ‘descubrir’ quiénes fueron los dos autores del robo basados en las respuestas que dieron. Recuerde que uno de ellos dijo dos nombres que no eran, y los cuatro restantes dijeron uno que estaba bien y otro que estaba mal.

Quiero empezar por A, ya que A es el único de los seis que está tan conectado (con tres “compañeros”) y ver qué se puede deducir de esto.

Supongamos que A no fue. ¿Qué se puede inferir?

Como A está ligado con B, D y E y sabemos que los autores fueron dos, esto significa que uno de estos tres (B, D o E) no fue tampoco. Es que no pueden haber sido los tres porque autores hubo nada más que dos. Entonces, tiene que haber por lo menos uno de estos tres que no fue.

Fíjese en la Figura 1. Mire los tres segmentos que salen desde A. Uno de esos tres segmentos une a dos que no fueron. Pero por otro lado, también en la Figura 1 se ve el segmento CF que tampoco fue. ¿Por qué? Porque los dos autores tienen que estar entre B, D y E. Esto es una contradicción porque habríamos encontrado dos segmentos que contienen dos personas de manera tal que ninguno fue. ¿De dónde provino este problema? Vino de haber supuesto que A no había sido uno de los autores. En consecuencia, hemos deducido que A fue uno de los que cometió el robo.

Ahora nos falta descubrir al segundo. Como A es uno de ellos, entonces se deduce que ni B, ni D ni E fueron autores también. ¿Por qué? Es que como están conectados con A (fíjese una vez más en la Figura 1) y ya sabemos que a lo sumo en cada segmento hay un solo autor, entonces esto excluye a B, D y E.

Nos queda por explorar qué sucede con C y con F.

Y acá viene algo interesante (y me permito sugerirle que piense usted en soledad para ver si podemos concluir juntos lo que sucede). Sigo.

Quiero proponerle que pensemos juntos si C fuera el otro autor. ¿Qué pasaría? Fíjese en todos los segmentos de la Figura 1. Como ya sabemos que A es uno de ellos, si C fuera el otro, entonces se deduciría que todos los segmentos tienen al menos un autor... ¡y eso no puede pasar! ¿Por qué? Porque de acuerdo con lo establecido originalmente, tiene que haber un par que no contenga a ninguno. Luego, si A y C fueran los dos autores, no habría manera de encontrar al tal par. Moraleja: la única alternativa que queda es que además de A, el otro autor sea F.

Y justamente eso es lo que pasa. Le sugiero que corrobore que todo funciona bien ahora. Si A y F son los autores, entonces los tres segmentos que unen a A con B, D y E lo tienen como único autor. El segmento CD es el único que no contiene a ninguno mientras que el último que falta considerar, el CF, este tiene a F como uno de los responsables.

De esta forma, con el análisis exhaustivo de todos los posibles casos es que llegamos al final. El dibujo que me/nos ayudó a representar la situación o a modelar la situación es lo que se llama un grafo. La matemática tiene una rama, nada menos, que se dedica a estudiar los distintos grafos y se llama (¿de qué otra forma si no?) Teoría de Grafos.

Policial o no, detectives o no, aquello que suele fascinar a muchísimas personas (descubrir al asesino) también tiene un correlato en la matemática, solo que por razones que van quedando atrás, ahora van apareciendo y emergiendo más y más. De hecho, es algo para celebrar.