[cerrar]

Comparta esta nota con un amigo

E-Mail de su amigo
Su nombre
Su E-Mail

Marzo del 2010. Una mañana cualquiera en Barracas. Un estudio de televisión como tantos otros en la Capital. Allí estábamos grabando uno de los capítulos de Alterados por Pi, el programa de matemática que se exhibe por el Canal Encuentro, en la Argentina. Claudio Martínez, el productor ejecutivo del programa, conversa en un costado con Woody González y Ariel Hassan, los realizadores y verdaderos artistas que lo hacen posible. En otro lado del estudio, Pablo Coll y Pablo Milrud repasan conmigo lo que voy a grabar. Ambos son matemáticos. Ambos monitorean lo que digo. Y, además, escriben una buena parte de los textos.

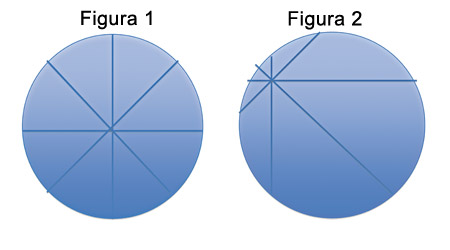
Me proponen que en el siguiente bloque muestre cómo la matemática puede ayudar para aprender a cortar una pizza. Supongamos que dos personas van a compartir una pizza grande. En general, la forma estándar de cortarla es la que se ve en la figura 1.

O sea, primero un corte por la mitad de la pizza, después otro perpendicular, también por la mitad y, después, dos cortes más, perpendiculares entre sí, y a 5 grados de los otros dos.

Claudio se acerca y escucha lo que me dicen “los Pablos”: “¿Por qué no mostrás que, usando muy poco de geometría, se puede probar que no hace falta cortar la pizza por la mitad, y después otra vez por la mitad, sino que se puede cortar en cualquier parte (no hace falta que sea en la mitad), y luego sí, hacer otro corte perpendicular en cualquier lugar, y después, seguir como en el caso convencional”.

Me preparo entonces para hacer unos dibujos en el pizarrón electrónico que tengo en el estudio, cuando Claudio me sorprende con una idea: “¿Por qué no aprovechamos y pedimos un par de pi-zzas? Vos podés cortar las dos en cámara y de esa forma será más descriptiva la explicación”.

“No”, le digo. “Claudio, si yo tengo que cortar las pizzas, nunca lo voy a poder hacer bien, vamos a necesitar 100 pizzas para hacerlo y me voy a tener que cambiar de ropa veinte veces. Dejame que lo haga en el pizarrón.”

Claudio insiste: “Ya sé. Tengo una idea. ¿Por qué no pedimos un par de pi-zzas acá a la vuelta, y le preguntamos si nos pueden mandar al pizzero para que las corte él. ¿Qué te parece?”. Eso sí me pareció muy astuto. Y acepté.

Una media hora más tarde, entró un joven con dos pizzas y un cuchillo enorme, obviamente recién afilado. Ya estaba maquillado, por lo que no había demasiado tiempo para perder. Le pregunté el nombre, y me dijo: “Luis”.

“Luis –seguí–, es muy sencillo lo que tenés que hacer. La primera pizza cortala como lo hacés siempre. En cambio, para la segunda, como yo quiero mostrar que no es imprescindible cortarla por la mitad, cortala de esta forma (y le relaté lo que figura más arriba).”

Luis me dijo que había entendido. Estaba nervioso, claro: luces, cámaras, sonidistas, iluminadores, productores, asistentes, gente de utilería... demasiado. Y todo junto. Le dije que no se preocupara, que era una grabación y que yo estaba allí para ayudarlo en lo que pudiera pasar. Sólo tenía que hacer lo que habíamos convenido.

Empezamos a grabar. Yo explico el problema –que de paso, invito a que usted trate de resolver (*)– y llega el momento para que Luis corte la primera pizza. Lo hace en forma impecable. En menos tiempo del que usted tarda en leer estas líneas, Luis cortó la pizza. Como hace siempre.

Con la segunda, ya fue otra historia. El primer corte, Luis lo hizo por la mitad (figura 6). Eso no me preocupaba tanto. El primer corte puede ser en cualquier parte, y si bien yo quería enfatizar que se podía cortar en cualquier parte, ese paso estaba bien.

Cuando llegó el momento de cortar otra vez, Luis lo quería hacer otra vez en la mitad. Es decir, seguir la rutina que utiliza en la pizzería. Y eso ya no nos servía (para el planteo que queríamos hacer).

Le dije: “No, Luis, cortá la pizza más arriba, da lo mismo en cualquier parte, pero más arriba”. Luis se resistía, porque en realidad, no me creía que la repartición sería equitativa entre las dos personas. Entonces, insistía en cortar en el medio otra vez.

Cuando le pedí nuevamente que cortara más arriba, me hizo caso, pero el lugar en donde él quería poner el cuchillo era demasiado cercano al medio, por lo que al final, si bien no era la mitad-mitad, la diferencia era imperceptible. No nos servía tampoco. Yo quería que fuera fácil percibir que no era un corte convencional.

“No, Luis. Cortá bien arriba, cerca del borde. No te preocupes”, le pedí.

Luis, que me quería ayudar y no creía en el argumento geométrico que yo quería exhibir, finalmente claudicó. Y se sometió a lo que yo le pedía. Pero eso sí: si bien el corte lo haría más arriba, ya no le importaba tanto “cómo”, y por lo tanto, empezó a hacer un corte que no era perpendicular al anterior.

Lo detuve y le dije: “No, Luis. Por favor, hacelo perpendicular”. Luis suspendió lo que estaba haciendo, y me miró como sorprendido. ¡Y ése fue un momento increíble para mí!

Por un instante, no entendí lo que pasaba. No entendía por qué había suspendido el corte. Pero, casi en forma inmediata advertí que con su mirada Luis me estaba diciendo que no entendía el significado de la palabra perpendicular.

Entonces, cambié y le dije: “A 90 grados, por favor Luis”. Pero Luis tampoco parecía entender lo que significaban “90 grados”.

Finalmente, le dije: ‘Luis, hacé una cruz”.

Eso sí resolvió el problema. De allí, fue todo fácil y terminamos la grabación sin más complicaciones.

Sin embargo, yo acababa de aprender una gran lección. Luis me había enseñado a prestar atención a algo muy importante. Luis estaba dispuesto a ejecutar cualquier cosa que yo le pidiera con la pizza. Pero claro, con una salvedad: ¡El tenía que poder entender lo que yo le pedía!

Toda esta historia, todo este relato, tenía como intención llegar a este punto. Por supuesto, los nombres y las referencias son todas ficticias, distorsionadas. El episodio sí existió, pero no con esos protagonistas. Pero la esencia de todo esto es que lo estoy invitando a pensar a usted, a todos los que hablamos con gente (o sea, casi todo el mundo), los que comunicamos (periodistas, docentes, padres)... ¿tenemos siempre claro que nuestro interlocutor entiende lo que le estamos diciendo? Las palabras se usan para comunicar algo. Pero si el lenguaje que usamos no sirve como mensajero, ¿por qué esperar que el otro pueda entenderlo? ¿Cuántas veces se frustró usted porque quiso decir algo y no lo/la comprendieron? ¿No habrá sido que el otro no comprendía el idioma que usaba?

¿Por qué dar por garantizado y/o aceptado, que la palabra “perpendicular” forma parte del vocabulario de todo el mundo? Y uso el ejemplo de la palabra perpendicular, porque es el que tengo a mano. Estoy seguro de que usted, mientras lee estas líneas, debe tener sus propios casos para elaborar.

Pocas veces me pasó que entendí algo en forma tan bruta y tan directa. Me sentí avergonzado, no tanto porque Luis no entendiera la palabra que yo usaba, sino por no haber tomado la previsión de que eso pudiera suceder. Con la matemática, históricamente, pasa algo así. El lenguaje que hemos usado hasta acá, ha sido –casi– como si hubiéramos hablado siempre en sánscrito. Y por eso, nada más que por eso, es que el “otro” parece que no entiende de qué se trata.

* Intente probar usted que no hace falta cortar por la mitad la pizza en ningún momento. Es suficiente hacer cuatro cortes perpendiculares de la forma en que se indica en el artículo, de manera tal que eligiendo adecuadamente las dos personas comen cuatro porciones cada una y terminan repartiéndose la pizza en partes iguales.