[cerrar]

Comparta esta nota con un amigo

E-Mail de su amigo
Su nombre
Su E-Mail

Lo que sigue es una propuesta para desafiar su intuición. Yo voy a plantear una situación hipotética y usted tendrá que decidir cuál de las respuestas que voy a ofrecerle (en una suerte de multiple choice) es la que más se aproxima a la verdad. Acá voy.

No sé si alguna vez se fijó en las medidas de una cancha de fútbol. Si no lo hizo, no tiene importancia: las escribo yo acá. El largo tiene que oscilar entre 90 y 120 metros y el ancho reglamentario tiene que estar entre 45 y 90 metros.

A los efectos del problema, voy a suponer que estamos en una cancha que mide exactamente 100 metros de largo. Yo traigo una soga que justo mide 100 metros y la ato a la base de uno de los postes verticales de uno de los dos arcos. Comienzo a caminar desplegando la soga, hasta que llego al otro lado, al otro arco, y con la soga bien tiranteQ, la ato a la base del poste que está exactamente enfrentado con el que elegí antes.

De hecho, como la soga tiene 100 metros de largo y la cancha también, debería suceder que la soga esté virtualmente pegada al césped a lo largo de todo el trayecto.

Hasta acá, todo bien. Sin embargo, hay algo que usted (que me está acompañando en el experimento) y yo advertimos: la soga está “muy tirante”. Sería conveniente agregarle unos centímetros, para darle un poco más de flexibilidad. Nos ponemos de acuerdo en agregarle 20 centímetros en total. O sea, ahora la soga mide 100,20 metros y nos deja un poco más satisfechos.

Acá es donde llega la pregunta que quiero hacerle: si caminamos hasta la mitad de la cancha y levantamos la soga “tanto como nos sea posible”, ¿qué cree que va a pasar?

a) la soga se levantará apenas unos centímetros del césped, tanto como para que quepa una mano abierta

b) la soga se levantará lo suficiente como para que usted pueda agacharse y deslizarse (o arrastrarse) por abajo de ella con su cuerpo pegado al pasto

c) la soga se levantará tanto que usted podrá caminar por abajo de ella sin esfuerzo

d) la soga se levantará tanto que usted podría venir con su auto y pasar por abajo.

Como ve, las cuatro alternativas son diferentes. No son exactas porque no sé bien ni cuánto mide usted, ni cuánto mide su auto (si es que tiene auto), ni cuál es la medida de su cuerpo se estuviera arrastrando por el suelo, pero si usted me concede la flexibilidad suficiente para interpretar el problema, verá que cada una de las variantes encuadra una situación diferente.

Dicho esto... y sin necesidad de hacer ninguna cuenta (al menos, al principio), ¿cuál de las cuatro posibilidades le parece que más se acerca a la respuesta correcta? En todo caso, ¿qué es lo que le dice su intuición?

Yo voy a seguir más abajo, pero créame (como no me canso de escribir): leer la respuesta es algo que usted siempre puede hacer. En cambio, poder medirse a uno mismo, saber cuán bien entrenada tiene la intuición, es algo que solamente lo puede hacer usted en soledad. No hay nadie que mire, no hay nadie que juzgue: solamente usted. ¿Qué tiene para perder? Por eso le digo: “ahora le toca a usted”.

Solución

Me encantaría poder estar en este momento pensando juntos. Podríamos compartir lo que le pasó (o le está pasando a usted) con lo que me pasó a mí la primera vez que me tropecé con este problema. Fue hace muchísimos años y tenía que ver con un ejemplo sobre la utilización del teorema de Pitágoras. Ya sé: si yo hablo de la necesidad de utilizar un teorema para explicar la solución, se produce un efecto inmediato: “¡esto no es para mí!”.

No crea. Es muy posible que sí sea para usted, aunque más no sea porque le va a permitir mejorar su capacidad para intuir. ¿No sería suficiente este hecho, o para querer averiguar qué es lo que me estoy perdiendo?

Como se imagina, puedo escribir acá y ahora cuál de las respuestas es la que más se acerca a la realidad, pero... ¿cuál fue la que eligió usted? ¿Y por qué?

Le cuento lo que me pasó a mí originalmente. Agregar ¡20 centímetros! a una soga de 100 metros, parece algo insignificante. De hecho “lo parece, porque lo

---

es”. Esto va a hacer que la soga no esté “tan tirante”, tal como era el objetivo.

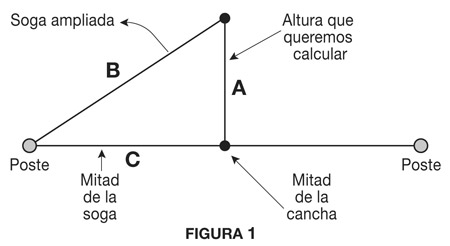
Ahora, vayamos hasta la mitad de la cancha y comencemos a levantarla. ¿Se podrá levantar mucho? Fíjese en el dibujo que aparece en la Figura 1. Como se ve, hice un esquema que sirve para graficar la situación. En principio, dibujé un triángulo de manera tal que cada lado represente una parte del problema.

El lado horizontal (C), corresponde a lo que mide la mitad de la cancha: 50 metros.

El lado que aparece “inclinado” (B), es el que correspondería a la soga después de haberle agregado 10 centímetros. Usted pensará ¿cómo 10 centímetros? ¿No habíamos agregado 20 centímetros? Sí, es verdad, pero 20 centímetros fue lo que agregamos al total de la soga, y por lo tanto, si estamos parados en la mitad de la cancha, la soga queda ampliada en la mitad de esos 20 centímetros y por eso el lado de la izquierda mide 50,10 metros, o sea, 50 metros más de 10 centímetros..

Por último, el lado vertical corresponde a la altura máxima que es la que queremos calcular. Es la altura a la que llegaríamos si tomáramos la soga que está atada a los dos postes, y alguien pudiera “levantarla desde arriba”. Ese número que llamé A (por altura) y es el que dio origen al problema.

Ahora bien: ¿cuánto mide A? Si usted se fija con cuidado, verá que el triángulo que quedó formado, es un triángulo particular. ¿En qué sentido es particular? Es que uno de los ángulos, mide 90 grados... ¿lo ve? Es el que forma el lado A con C (el horizontal). Justamente, hicimos todo lo posible para poder levantar la soga lo más alto que pudiéramos y ahora, queremos medir cuál es la distancia que hay desde ese punto “más alto” con el césped. Hemos descubierto entonces que el triángulo que nos ocupa, es lo que se llama un triángulo rectángulo.

¿Y? ¿Qué agrega ese dato? Bueno, agrega algo muy importante. Agrega un dato que nos permite, a usted y a mí, usar el teorema de Pitágoras. ¿Por qué? Porque el teorema de Pitágoras dice justamente cómo están relacionados los tres lados del triángulo. Es decir, establece una conexión entre esos tres números (las medidas de los lados), pero esta fórmula (que usted debe haber escuchado hasta el hartazgo**) no vale para cualquier triángulo sino que solamente se puede aplicar a triángulos que tengan un ángulo recto. Lo bueno de esto es que justamente estamos en presencia de un triángulo rectángulo que tiene un ángulo recto (y que por eso se llama rectángulo).

Usando la fórmula, cuando uno conoce dos de los tres lados, puede deducir el tercero:

B2 = A2 + C2 (*)

Ahora, mire la Figura 2 en donde aparece otra vez el triángulo. El lado horizontal C mide 50 metros y el lado B (que lleva el nombre de “hipotenusa”) mide la “soga ampliada” (50,10) metros. Esto quiere decir que B = 50,10 metros y C = 50 metros. Reemplacemos la igualdad (*) con los números que correspondientes y le recuerdo que el número que no sabemos es el que llamé A (que corresponde a la altura). Se tiene entonces:

(50,10)2 = A2 + (50)2

A2 = (50,10)2 (50)2

A2 = 2510,01 2500 = 10,01.

Y estamos a punto de terminar el cálculo. Ya sabemos entonces cuánto mide el cuadrado de A (o sea, A2). Para poder calcular A, lo que necesitamos es extraer la raíz cuadrada del número (10,01), muy fácil si uno tiene una calculadora a mano. Si no, escribo yo lo que da: (aproximadamente) 3,16.

Es decir, el lado A mide... (increíblemente... al menos para mí) más de 3,15 metros, lo que ofrece lugar suficiente no solo para poner una mano, o arrastrarse por el césped o incluso caminar por abajo, sino hasta para poder traer un auto y manejarlo por abajo de la soga levantada.

¿Atenta esto contra la intuición? Creo que sí, pero me es fácil sacar conclusiones mientras yo estoy solo y sin contar con su presencia. A usted, ¿qué le pasó? ¿Valió la pena hacer el cálculo? ¿Qué aprendió al pensar el problema? Usted dirá....

* Concédame la licencia de que la soga tenga algunos centímetros más como para que me permita atar cada extremo en cada uno de los postes, pero de tal forma que la parte que queda horizontal, mida exactamente 100 metros.

** En todo triángulo rectángulo, el cuadrado de la hipotenusa (B) es igual a la suma de los cuadrados de los catetos (A y C en este caso), o sea: B2 = A2 + C2. Esa es la forma en la que están relacionados esos tres números. Si usted conoce dos de ellos, puede averiguar el tercero.