[cerrar]

Comparta esta nota con un amigo

E-Mail de su amigo
Su nombre
Su E-Mail

Cualquiera que viva en una gran ciudad de la Argentina va a entender esto: el tránsito está transformándose cada vez más en una gran “aventura”.

- Cruzar las calles obliga a un constante gesto de audacia.

- Manejar, también.

Ahora bien, ¿por qué sucede que en algunos países el tránsito es más ordenado y en otros es más caótico?

Yo sé que la respuesta que surge inmediatamente es la de la educación. Y es natural que así sea. Ser peatón en Suiza no es lo mismo que en Córdoba o Buenos Aires. Y manejar en Munich involucra muchísimos menos riesgos que en Rosario o Tucumán. Pero también es cierto que el respeto que existe por “el otro” en cada una de las ciudades europeas es diferente del que existe en nuestro país.

Me quiero ocupar específicamente del tránsito vehicular. Y lo quiero hacer desde dos perspectivas diferentes: desde la del conductor del vehículo y desde la del planificador, o sea, desde aquel que quiere “organizar y poner las reglas” para que manejar no se transforme en un acto que orilla entre el homicidio y el suicidio.

La matemática puede servir para mejorar las condiciones de vida de la sociedad, mientras nos “educamos” y aprendemos a ser más solidarios y respetuosos con “el otro”. La idea es entonces “modelar” el problema y tratarlo con las herramientas adecuadas.

Pongámonos de acuerdo en lo siguiente. El tránsito de vehículos sería ideal si le permite al conductor llegar a destino

1 en el menor tiempo posible;

2 con el menor riesgo posible;

3 minimizando el costo (teniendo en cuenta combustible, peaje, infracciones, etc.);

4 sin estresarse.

Obviamente, entre el tránsito ideal y el real hay fuertes diferencias.

El que conduce no está solo. Maneja con otros alrededor. Por lo tanto, si cada uno de ellos intenta optimizar los cuatro puntos, eso va a terminar afectando las condiciones de “los otros”. Es decir, algunos de los puntos se ponen “en tensión”.

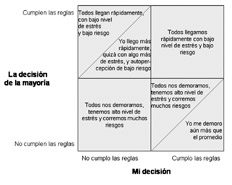
Por ejemplo, uno puede llegar a su destino más rápidamente (optimizando el primer punto), pero para hacerlo tiene que ir por una autopista en lugar de por calles internas y eso empeora el punto 3. O, en cambio, puede optar por ir por un camino más largo pero más seguro, por lo que está privilegiando los puntos 2 y 4, pero empeora los puntos 1 y 3, porque tarda más y consume más combustible (ver la figura).

Pero, además de elegir el camino, el conductor toma un gran número de decisiones en muy poco tiempo. Por ejemplo: el semáforo se puso en amarillo, ¿frena o acelera? ¿Esquiva el pozo o lo pasa por arriba? ¿Pone la señal de giro para pasar de carril o no? ¿Respeta el carril? Si alguien pone la luz de guiño para doblar delante de él, ¿desacelera para dejarlo pasar o acelera para que “no le gane”? ¿Mira para adelante o por el espejo retrovisor o al tablero o a la persona que viene en el asiento del acompañante?

Como se ve, hay muchísimas variables que pasan inadvertidas porque terminan siendo decisiones “casi” inconscientes, que se toman automáticamente.

La matemática permite predecir cómo se va a comportar el tránsito. Sí, aunque suene antiintuitivo, es posible construir un “modelo” que replique la realidad en forma tan aproximada que uno pueda sacar conclusiones sobre lo que “va a pasar”, antes de que suceda.

Uno, en tanto que conductor, “cree” que hace lo que quiere. Hasta cierto punto, eso es cierto. Pero el tránsito y el flujo vehicular “toma decisiones” por uno sin que sean advertidas por el que maneja.

En general, la rama de la matemática conocida con el nombre de Teoría de Juegos sirve para entender un poco más el problema. En realidad, como casi todos los países tienen reglas de tránsito bastante desarrolladas, el grado de cumplimiento de esas reglas es lo que varía y lo que genera diversos conflictos que podrían ser superados si la cultura fuera diferente. Incluso dentro de un propio país, habitantes de distintas ciudades respetan las reglas en forma diversa.

Por ejemplo, en una cultura en la que hay un alto nivel de acatamiento, en general, el promedio de los conductores llega más rápidamente a destino, lo hace con menos estrés y con mucho menos riesgo de accidentes. Estas situaciones se llaman de colaboración.

Por supuesto, lo inverso sucede en culturas con bajo grado de acatamiento, es decir, en situaciones de no colaboración.

La pregunta que cada conductor se hace –consciente o inconscientemente– es, “¿cuál va a ser mi grado de acatamiento de las reglas de tránsito?”.

De las respuestas que se obtengan, y de la matemática, dependerá la elaboración de un plan de tránsito.

Lo invito a pensar entonces en dos situaciones posibles. En la Argentina, donde el nivel de acatamiento a las reglas de tránsito es en general muy bajo, como conductor uno tiene dos opciones:

- Usted puede hacer como todos los demás, o sea, no cumplir las reglas, y por lo tanto, demorar en llegar a destino, estresado y con alto riesgo de accidentes...

- O bien, usted puede cumplir con las reglas, pero el grado de estrés puede incluso aumentar (por el fastidio que le genera ver lo que hacen todos los demás) y, además, posiblemente también termine demorando más en llegar a su destino.

Ante esta disyuntiva, la mayoría de la gente se contagia de la cultura local y deja de cumplir la mayoría de las reglas.

¿Qué sucede en otras culturas? Suponga ahora que usted está en Suecia o Alemania, en donde hay un alto nivel de acatamiento a las reglas de tránsito. Uno también tiene dos opciones (como conductor).

- Se alinea con lo que ve y cumple con las reglas, en cuyo caso tiene el mismo beneficio que los otros que están al volante...

- O bien decide no cumplir con algunas reglas para aprovecharse de esa cultura y así llegar más rápidamente que todos los demás, quizá con un poco más de estrés, y seguramente con una percepción de que no incrementó mucho más su riesgo.

En principio, parecería que la segunda opción, en la que uno “se aprovecha del sistema”, es la mejor, ya que uno tiene todos los beneficios como si hubiera respetado las leyes y, encima, llega antes.

Pero el problema reside en que si todos llegan a la misma conclusión que usted y deciden no cumplir con las reglas, entonces uno ha logrado cambiar la cultura y termina en el peor de los escenarios.

Aunque no lo parezca, alcanza con que entre el 5 y el 20 por ciento deje de cumplir las leyes para que la cultura cambie dramáticamente de una situación de colaboración a una de no-colaboración.

Y una vez que se rompe la cultura de la colaboración es muy difícil restituirla, ya que los que cumplen y se ven perjudicados por cumplir no tienen el incentivo para seguir respetando las reglas por miedo a que los demás se aprovechen de ellos. Entonces, todo sigue igual: mal.

Con modelos muy similares al que acabo de describir para el tránsito, se pueden entender dinámicas de colaboración y no-colaboración en el pago de impuestos, en la corrupción, en el trabajo en equipo en empresas y en muchos otros ámbitos sociales.

Por otro lado, la matemática es también esencial para poder diseñar y planificar el tránsito en una ciudad o en un país. Por ejemplo, piense usted si tuviera que tomar alguna de estas decisiones:

- ¿Será conveniente construir una autopista?

- ¿Y en dónde poner el peaje?

- ¿O convendrá expandir una línea de subte?

- ¿O incluso no sería mejor cambiar el recorrido de un colectivo?

- ¿Dónde convendría agregar semáforos?

- ¿Y en dónde permitiríamos estacionar y en dónde no?

- ¿Convendría construir un nuevo puente?

- ¿O modificar la velocidad máxima en una autopista?

Todas estas decisiones deberían estar basadas en poder predecir qué reacciones van a producir una vez implementadas (más allá de las cuestiones económicas que involucran). La aspiración es que cada cambio sea un cambio positivo, pero ¿cómo garantizarlo? La matemática permite modelar estos cambios, fijarse qué tipo de reacciones se producen y evaluar si vale la pena hacerlos o no. Por supuesto, además de mejorar la experiencia del transporte, se necesita evaluar otras variables como el nivel de ruido, la contaminación que se agrega, el costo de inversión para una obra o incluso una modificación reglamentaria.

Y es allí donde una vez más se hace imprescindible el uso de herramientas de simulación y optimización y, por supuesto, la resolución de ecuaciones que describen el problema. Y todo esto es hacer matemática. Una vez más.

* El Dr. Gerardo Garbulsky es quien inspiró y pensó este artículo. Sin él, yo no lo hubiera podido escribir. Su trabajo se vio reflejado también en la serie Alterados por Pi, que se emite por el canal Encuentro, en donde Gerardo participa como coautor.